A crease pattern can be flat-foldable if all of the following conditions are upheld:
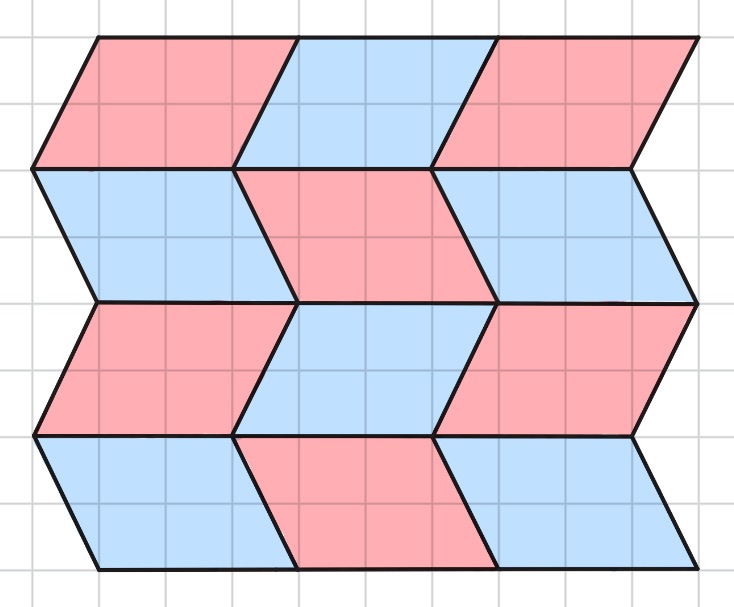
Two-Colourability
The crease pattern must be two-colourable. This is because, when the crease pattern is folded flat, there must be a number of panels facing up, and others facing down, each separated by creases. In this way, adjacent panels are oppositely situated. The two colours represent these two states. This is a global condition, as it applies to the whole pattern, not just to one vertex. However, while a pattern that is not two-colourable is certainly not flat-foldable, the opposite does not necessarily hold true.
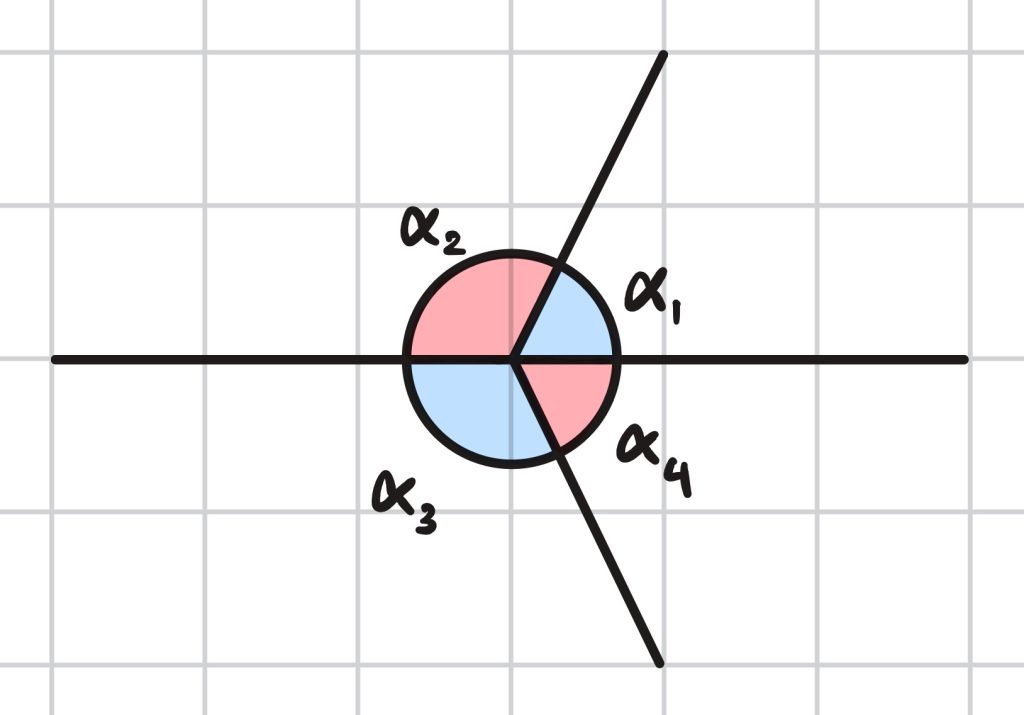
Kawasaki’s Theorem
Kawasaki’s Theorem must hold true for every vertex. This constrains the angles around a vertex: For a vertex with an even number of creases, α₁ + α₃ + … = α₂ + α₄ + … = 180° This confirms that a vertex can flatten without bending the material, which is a common property of a flat-foldable pattern. However, this only applies to each vertex individually, not the whole crease pattern.
Maekawa’s Theorem
Maekawa’s Theorem must hold true for every vertex. This refers to the number of mountain and valley folds around each vertex: The number of mountain and valley folds around a vertex must differ by two, such that |M-V| = 2 This confirms that a vertex is able to be folded flat by expressing the angle of each fold as ±180º, resulting in an overall 360º rotation for flat-foldability.
No Self-Intersection
Finally, a crease pattern cannot intersect itself while in the process of being flat-folded, so not all theoretically flat-foldable patterns can exist in the real world.